이번에는 이렇게 찾은 외곽선을 근사화 하는 알고리즘에 대해 알아보도록 하겠습니다.
Ramer Douglas Peucker algorithm 또는 iterative end-point algorithm 이라고 불리는 DP 알고리즘은 line segment들로 이루어진 곡선이나 다각형을 근사화하는 알고리즘으로 많이 사용되는 알고리즘 입니다.
컨셉이 간단하고 강력하기 때문에 꼭 알아두시면 좋은 알고리즘입니다.
DP 알고리즘 원리
다각형 또는 곡선은 여러개의 vertex로 이루어져 있습니다. 이 꼭지점들을 하나의 vector로 만들어 놓았다고 가정합니다.
일단 알고리즘을 다각형으로 설명을 드리면 곡선은 자연히 이해가 되실 거 같아 아래와 같은 다각형으로 설명드리겠습니다.
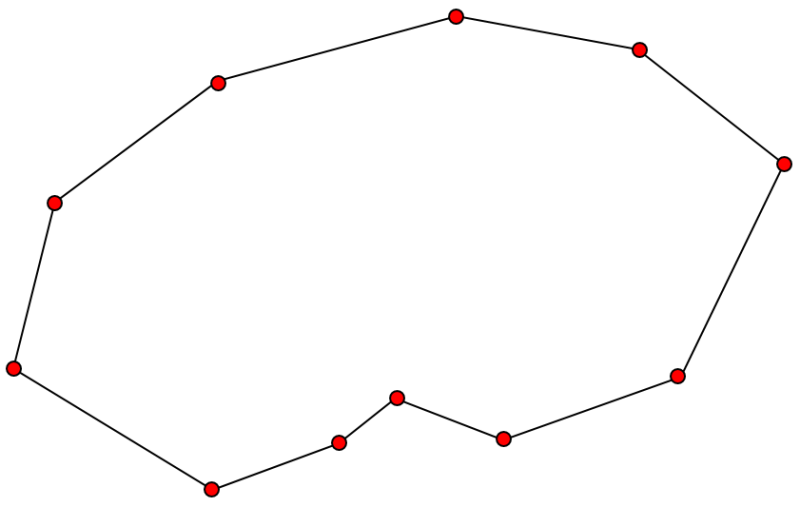
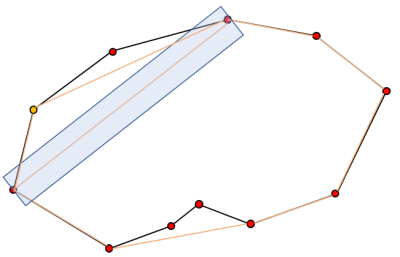
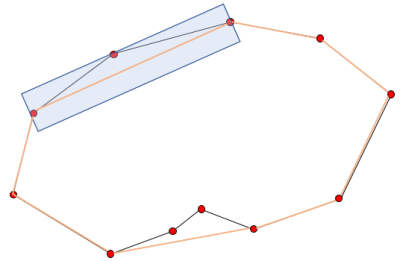
1. 점들중 가장 멀리 떨어져있는 두 점을 찾고 두 점을 잇는 직선의 식을 계산한다.
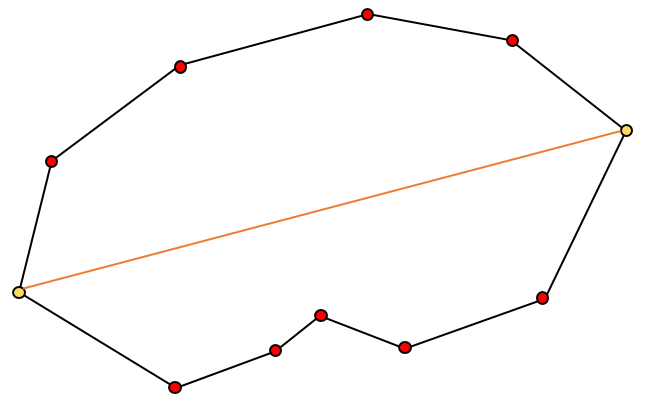
2. 두 점을 잇는 직선과 가장 멀리 떨어져있는 꼭지점(vertex)를 찾는다. 단 직선과의 거리가 우리가 설정한 epsilon 값(임계치) 보다 커야 한다.
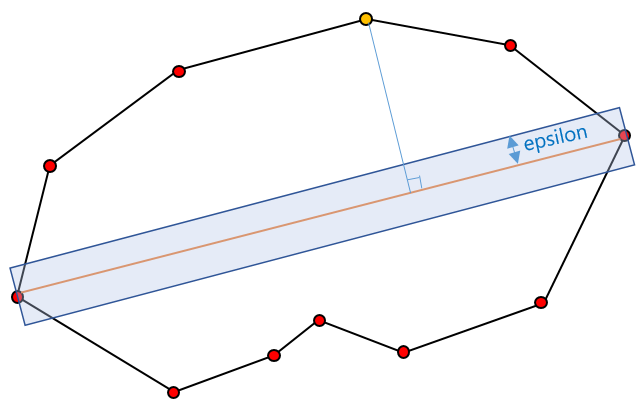
3. 거리가 임계치보다 크다면 양 끝점에서 새로운 점과 연결선을 생성한다. 3개의 선분이 생겼을 것이다.
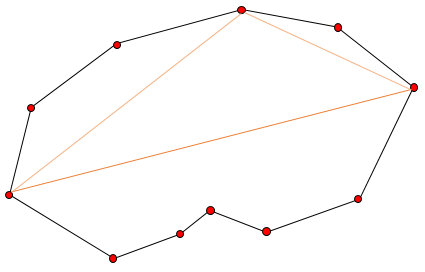
4. 다시 한 선분 과 다른 점들과의 거리를 계산하여 가장 멀리 있는 점을 선택하여 조건(임계치 이상)에 맞는다면 선분을 연결한다.
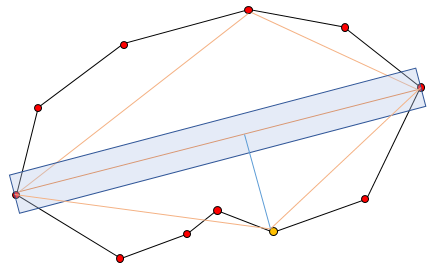
5. 새로 생긴 선분에서 또 가장 멀리 있는 점을 선택하여 조건에 맞는다면 선분을 연결한다.
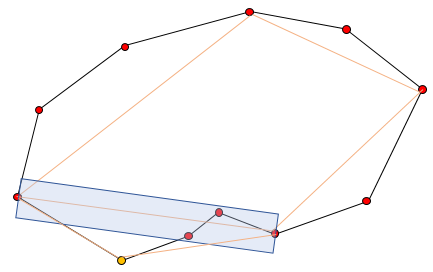
6. 재귀적으로 새로 생긴 선분에서 가장 멀리 있는 점을 찾아 선분을 연결하는 작업을 반복한다.
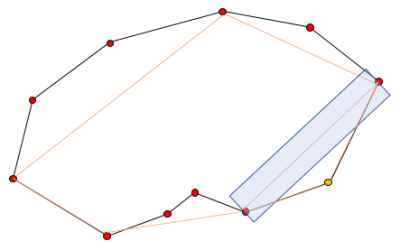
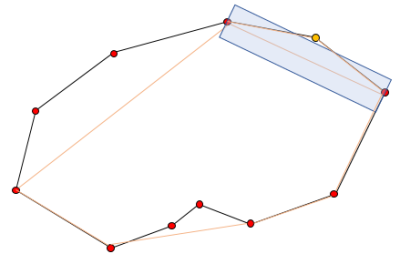
7. 모든 점에 대해 간소화를 한 결과는 아래와 같습니다.
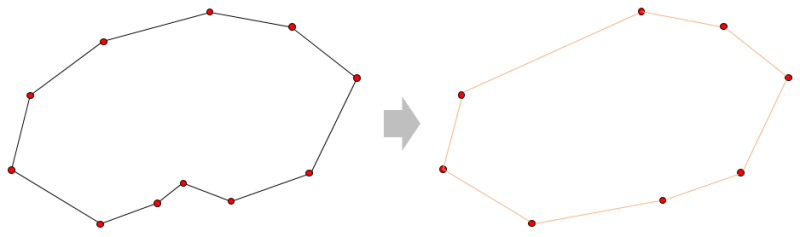
이 절차를 C++ 소스로 구현하면 아래와 같은 함수를 만들 수 있습니다.
재귀 호출을 사용하면 쉽게 구현이 되겠죠?
일단 시작점과 끝점이 주어지면 그 직선과 점과의 거리를 계산하는 함수를 하나 만들고, 재귀 호출 기법을 이용한 DouglasPeucker 알고리즘을 구현하였습니다.
pointList_in 으로 cv::Point 형태의 점들의 vector를 입력하면, pt_out으로 간략화된 새로운 점들의 결과를 출력합니다.
아래 소스는 github를 참조하였습니다.(https://gist.github.com/TimSC/0813573d77734bcb6f2cd2cf6cc7aa51)
'IT, 프로그램, SW개발 > 알고리즘' 카테고리의 다른 글
| 간단한 단위변환 계산기 만들기 (코드) (0) | 2025.09.16 |
|---|---|
| DFS, BFS 스터디용 (0) | 2021.02.05 |
| 트라이(Trie)알고리즘 (0) | 2020.04.07 |

